Моделируем вселенную: небесная механика наглядно

Моделируем вселенную: небесная механика наглядно

Давайте представим, что нам нужно запустить футбольный мяч на орбиту Земли. Никакие ракеты не нужны! Хватит горы, высотой 100 километров и недюжинной силы. Но насколько сильно нужно пнуть мяч, чтобы он никогда больше не вернулся на Землю? Как отправить мяч в путешествие к звёздам, имея только грубую силу и знание небесной механики?

Сегодня в программе:

• Бесконечные возможности одной формулы
• Как взять энергию у Юпитера
• Откуда у планет берутся кольца
• Как математика помогла открыть Нептун

Благо, мы живём в век компьютерных технологий. Нам не нужно забираться на высокую гору и пинать мяч со всей силы, всё можно смоделировать! Давайте приступим.

Одна формула

Та самая, известная с уроков физики и астрономии:

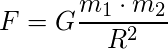
Показывает, насколько сильно будут взаимодействовать тела, в зависимости от их масс, расстояния между ними и гравитационной постоянной G.

Я написал программу, в которой можно расставлять шарики, взаимодействующие друг с другом силами гравитации, при этом у каждого шарика есть своя масса, скорость и координаты. Для наглядности шарики оставляют за собой след.

Давайте поставим большой и массивный голубой шар(Землю) и маленький красный мячик недалеко от него. Запускаем симуляцию:

Для выхода на орбиту нужна скорость, чтобы шарик падал и все время промахивался мимо Земли. Но КАКАЯ скорость? И снова школьные знания приходят на помощь:

Минимальная скорость, необходимая для выхода на орбиту Земли называется первой космической скоростью.

Для Земли она равна 7.91 км/с. А для симуляции её можно легко вычислить:

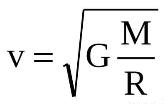
Разгоняем мячик и смотрим результат:

Шарик описывает окружность с Землёй в центре. Что будет, если придать ему чуть больше скорости? Сейчас проверим:

Теперь форма орбиты эллиптическая, можно выделить 2 очень важные точки — апогей и перигей.

Апогей — это точка, в которой мячик максимально удалён от Земли.

Перигей — наоборот, самая близкая к Земле точка.

При увеличении начальной скорости перигей не меняется, а вот апогей становится всё дальше, и в конце концов имеет бесконечное расстояние до Земли. Тут мы вплотную приблизились к понятию второй космической скорости. Это скорость, которую надо придать шарику, чтобы он преодолел гравитацию Земли и улетел бороздить просторы вселенной. Для земли она равна 11.2 км/с.

Интересный фокус: если мы умножим первую космическую скорость на √2, то получим вторую космическую.

Умножили. Запустили. Получили:

Он улетел безвозвратно! Кстати, теперь он имеет параболическую орбиту. А если запустить шарик ещё сильнее, получим гиперболу. Интересно получается, везде нас преследует математика.

При этом формула остаётся всё той же. Окружность превращается в эллипс, эллипс в параболу, а парабола в гиперболу из-за вытягивания орбиты(увеличения эксцентриситета).

Как взять энергию у Юпитера?

Давайте расширим нашу модель, добавим Солнце, заставим Землю крутиться вокруг него.

Представим, что мячу нужно придать такую скорость, чтобы он улетел за пределы Солнечной системы — третью космическую скорость. В реальном мире она равна 16.7 км/с. К сожалению, эта скорость слишком большая, боюсь, нам не хватит сил…

Постойте! А что, если забрать немного скорости у какого-нибудь массивного тела, например, Юпитера. Мы можем подлететь к чему-то очень массивному и совершить гравитационный манёвр. При пролёте мимо Юпитера силы гравитации взаимно притягивают мячик и газовый гигант, но масса мячика настолько мала, что почти никак не влияет на движение Юпитера, а сам Юпитер разгоняет пролетающее мимо тело до высоких скоростей.

Меньше слов — больше дела:

Момент гравитационного манёвра — шарик подлетел к Юпитеру.

Ура! Мы получили скорость, достаточную для выхода из Солнечной системы, при этом ничего не потратили. Правда, Юпитер стал двигаться чуть медленнее, но мы этого точно не заметим.

Все космические аппараты, запущенные человеком за пределы солнечной системы («Вояджеры» 1 и 2, «Пионеры» 10 и 11, «Новые горизонты») использовали именно такой способ для ускорения.

Задачи небесной механики

Основная задача небесной механики заключается в расчёте движения небесных тел под действием сил всемирного тяготения. В эту задачу включают исследование и расчёт движения планет, искусст­венных спутников Земли (ИСЗ), космических аппаратов, звёзд в двойных и кратных системах, строения галактик. Среди них наиболее популярной и классической является задача n тел.

В число задач небесной механики включают и учёт приливных сил, возникающих вследствие неоднородности поля тяготения.

Все эти задачи в математическом смысле исключительно трудны. Большинство из них решается численными методами с использованием самых мощных компьютеров. Но есть и задачи, ко­торые могут быть решены в аналитическом виде.