Особенности движения планет вокруг Солнца

Особенности движения планет вокруг Солнца

Движение планет вокруг Солнца задает бег карусели нашей Солнечной системы. А скорость и направление вращения во многом помогли успешному появлению и развитию жизни на Земле. Однако в течение многих столетий на нашей планете царствовала геоцентрическая теория, утверждавшая, что Солнце вращается вокруг Земли. Польский ученый Николай Коперник доказал несостоятельность этой доктрины, хотя и пострадал от своих революционных для того времени идей.

Сегодня нам вовсе не нужно оспаривать церковные догматы, ведь мы прекрасно знаем, что именно вокруг Солнца вращаются все остальные планеты нашей системы. Но как именно они движутся? Почему движение нашей планеты позволяет ей поддерживать равномерную температуру, в то время как на гигантах Солнечной системы градусник буквально зашкаливает то в плюс, то в минус? Что заставляет планеты двигаться по таким разнообразным орбитам?

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока “Законы движения планет Солнечной системы”

Вы уже знаете, что революционная идея Николая Коперника о гелиоцентрической системе мироустройства дала невероятный толчок развитию астрономии. Однако, если вы помните, Коперник в своём учении не отказался от мыслей Аристотеля о “совершенстве” орбит планет. Поэтому для объяснения многих явлений (например, попятного движения планет), в его теории всё ещё присутствовали эпициклы и деференты.

При этом многие учёные считали, что движение небесных тел должно быть равномерным и по «самой совершенной кривой», то есть окружности. Поэтому до конца XVI века им не удавалось точно рассчитать относительное положение планет на несколько лет вперёд. Теория давала заметное расхождение с результатами наблюдений.

Лишь в начале XVII века австрийский астроном Иоганн Кеплер открыл кинематические законы движения планет. В своих поисках он исходил из убеждения, что «в мире правит число», высказанного ещё Пифагором. Кеплер пытался сопоставить характеристики движения планет с закономерностями музыкальной гаммы, длиной сторон, описанных и вписанных в орбиты планет многоугольников и так далее.

Но увы, каждый раз сравнив свою модель с наблюдаемыми орбитами планет, Кеплер вынужден был признавать, что их реальное поведение не вписывается в очерченные им стройные рамки. По меткому замечанию современного британского биолога Джона Холдейна, «идея Вселенной как геометрически совершенного произведения искусства оказалась ещё одной прекрасной гипотезой, разрушенной уродливыми фактами».

Лишь переехав в Прагу и став учеником датского астронома Тихо Браге, Кеплер натолкнулся на идеи, по-настоящему обессмертившие его имя в анналах науки.

Представим себе проблему, с которой столкнулся Кеплер, следующим образом. Мы находимся на планете, которая, во-первых, вращается вокруг своей оси, а во-вторых, обращается вокруг Солнца по неизвестной нам орбите. Глядя в небо, мы видим другие планеты, которые также движутся по неизвестным нам орбитам. Вопрос: как по данным наблюдений, сделанных на одном вращающемся вокруг оси и вокруг Солнца шарике, определить орбиту и скорость движения других планет?

Кажется, что вопрос достаточно сложный, даже при современном уровне компьютеров. А у Кеплера их не было и, тем не менее, ему удалось найти ответ!

Наблюдая за движением Марса в пространстве, а также воспользовавшись многолетними определениями координат и конфигураций этой планеты, проведёнными Тихо Браге, Кеплер обратил внимание на то, что Марс движется неравномерно. Он решил построить орбиту Марса. Для этого он сделал небольшое приближение, посчитав орбиту Земли круговой (что не противоречило наблюдениям). Затем он рассуждал примерно так. Пусть нам известно угловое расстояние Марса (точка М на рисунке) от точки весеннего равноденствия во время одного из противостояний планеты, то есть его прямое восхождение α₁.

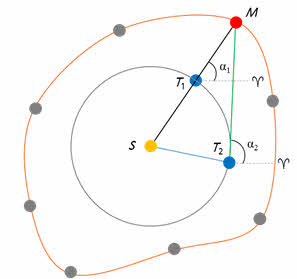
Т₁ — это положение Земли во время противостояния с Марсом.

Для того, чтобы Марс оказался вновь в этой же точке своей орбиты, должно пройти 687 суток (таков звёздный период обращения Марса). Сидерический же период Земли равен 365 суткам. Поэтому, она не успеет «добежать» до точки T₁ и в этот момент будет находиться на своей орбите в точке Т₂. Следовательно, для наблюдателя измениться прямое восхождение Марса. Так вот раз за разом изучая различные противостояния Марса Кеплер получил целый ряд точек. Соединив их плавной кривой, он построил орбиту этой планеты, которая, как оказалось, не являлась окружностью.

Теперь Кеплер был поставлен перед необходимостью сделать выбор одного из двух возможных решений: считать, что орбита Марса представляет собой окружность, и допустить, что на некоторых участках орбиты вычисленные координаты планеты расходятся с наблюдениями; или же считать, что все наблюдения были правильными, а орбита планеты действительно не является окружностью. Будучи уверенным в точности своих наблюдений и наблюдений Тихо Браге, Кеплер выбрал второе решение и установил, что наилучшим образом положения Марса на орбите совпадают с кривой, которая называется эллипсом. При этом Солнце располагается не в его центре. В результате им был сформулирован закон, который впоследствии назвали первым законом Кеплера: все планеты обращаются по эллипсам, в одном из фокусов которых находится Солнце.

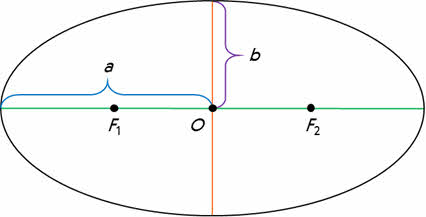
На рисунке точка О — это центр эллипса, а F₁ и F₂ — его фокусы.

Проходящий через фокусы эллипса отрезок, концы которого лежат на эллипсе, называется его большой осью.

А отрезок, проходящий через центр эллипса перпендикулярно большой оси, называется малой осью эллипса.

Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях, называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются малыми буквами a и b.

Отличие эллипса от окружности характеризуется величиной его эксцентриситета. Он равен половине отношения фокусного расстояния эллипса к его большой полуоси:

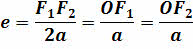
Отметим, что в случае, когда эксцентриситет эллипса равен нулю, фокусы и центр эллипса сливаются в одну точку — эллипс превращается в окружность.

Теперь предположим, что Солнце расположено в фокусе F₁. Тогда ближайшая к Солнцу точка орбиты планеты называется перигелием. А наиболее удалённая от Солнца точка, называется афелием.

Например, у земной орбиты эксцентриситет равен 0,017, то есть орбита действительно почти круговая. В перигелии наша планета находится в начале января. Расстояние до Солнца составляет около 147 миллионов километров. Афелий Земля проходит в начале июля, а афелийное расстояние составляет чуть более 152 миллионов километров.

Но вернёмся к Кеплеру и построенной им траектории Марса. Изучив расположения полученных точек, он увидел, что скорость Марса по орбите меняется. Но при этом радиус-вектор планеты (то есть линия, соединяющая центр Солнца с центром планеты) за равные промежутки времени описывает равновеликие площади.

Обнаруженная закономерность впоследствии получила название второго закона Кеплера (иногда его называют законом площадей).

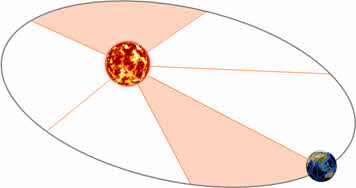
Чтобы лучше понять его физический смысл, вспомните своё детство. Наверняка, вам доводилось на детской площадке раскручиваться вокруг столба, ухватившись за него руками. Фактически, планеты обращаются вокруг Солнца аналогичным образом. Чем дальше от Солнца уводит планету эллиптическая орбита, тем медленнее движение, чем ближе к Солнцу — тем быстрее движется планета.

Объяснить данный закон можно на основе закона сохранения энергии. Из физики вам известно, что полная механическая энергия замкнутой системы тел, между которыми действуют силы тяготения, остаётся неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергий планеты, которая движется вокруг Солнца, неизменна в каждой точке орбиты планеты. Приближаясь к Солнцу потенциальная энергия планеты уменьшается, в следствии уменьшения расстояния до Солнца. Поэтому её кинетическая энергия должна увеличиваться. А сделать это можно лишь за счёт увеличения скорости.

Таким образом, скорость движения планеты по орбите меняется, принимая максимальное значение в перигелии и минимальное в афелии.

Первый и второй законы были опубликованы Кеплером в 1609 году в книге «Новая астрономия, или Физика небес, изложенная в исследованиях движения планеты Марс. ». Хотя реально первый закон Кеплера был открыт в тысяча шестьсот пятом 1605 году, а второй — тысяча шестьсот втором 1602.

Свой третий закон Кеплер сформулировал лишь в 1618 году. Он гласит, что квадраты сидерических периодов обращения двух планет относятся как кубы больших полуосей их орбит:

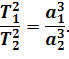
Вот что писал по этому поводу сам Кеплер: «То, что 16 лет тому назад я решил искать, наконец найдено, и это открытие превзошло все мои самые смелые ожидания. ».

И действительно, третий закон заслуживает самой высокой оценки. Ведь он позволяет вычислить относительные расстояния планет от Солнца, используя уже известные их периоды обращения вокруг него. При этом не нужно вычислять расстояния от Солнца до каждой планеты, достаточно измерить это расстояние для одной из них, например, Земли. Кстати, для простоты вычислений, величину большой полуоси́ орбиты Земли приняли равной одной астрономической единице (1 а. е.). Эта единица измерения стала основой для вычисления всех остальных расстояний в Солнечной системе.

Ещё раз обратим ваше внимание на то, что Кеплер открыл свои законы исходя только из собственных наблюдений, и наблюдений Тихо Браге. Если бы вы спросили его, чем обусловлена эллиптичность орбит или равенство площадей секторов, он бы вам не ответил. Это просто следовало из проведённого им анализа. Если бы вы спросили его об орбитальном движении планет в других звёздных системах, он также не нашёл бы ответа на этот вопрос.

Однако гений Кеплера в том и заключался, что он смог увидеть то, во что остальные отказывались верить. А строгое математическое доказательство его законы получили лишь после того, как Ньютоном были открыты закон Всемирного тяготения и закон сохранения момента импульса (известный нам второй закон Ньютона). Но об этом в следующий раз. А сейчас давайте решим с вами одну небольшую задачку. Определите период обращения астероида Россия, если большая полуось его орбиты равна 2,55 а. е.

Лекция по астрономии. законы движения планет

Дисциплина « Астрономия »

Специальность 08.02.01 «Строительство и эксплуатация зданий и сооружений»

курс III группа: 1с1, 2с1, 3с1, 4с1

Преподаватель: Жданова Наталия Владимировна

ЛЕКЦИЯ 7. Законы движения планет Солнечной системы. (2 часа)

План лекции:

Законы Кеплера

Иоганн Кеплер (рис. 4.3) определил, что Марс движется вокруг Солнца по эллипсу, а потом было доказано, что и другие планеты имеют эллиптические орбиты.

Первый закон Кеплера . Все планеты обращаются вокруг Солнца по эллипсам, а Солнце находится в одном из фокусов этих эллипсов (рис. 4.4, 4.5).

Рис. 4.4. Планеты обращаются вокруг Солнца по эллипсам. AF ₁ =F _min — в перигелии; BF ₁ =F _max — в афелии

Главное следствие из первого закона Кеплера: расстояние между планетой и Солнцем не остается постоянным и изменяется в пределах: r _max ≤ r ≥ r _min

Точка А орбиты, где планета приближается на наименьшее расстояние к Солнцу, называется перигелием (греч. peri — вблизи helios — Солнце), а самую отдаленную от центра Солнца точку В орбиты планеты назвали афелием (от греч. аро — вдали). Сумма расстояний в перигелии и афелии равна большой оси АВ эллипса: r _max + r _min = 2a. Большая полуось земной орбиты (ОА или ОВ) называется астрономической единицей . 1 а. е. = 149,6×10 6 км.

Земля в перигелии 3—4 января приближается к Солнцу на наименьшее расстояние 147 млн км

Земля в афелии 3—4 июля удаляется от Солнца на самое большое расстояние 153 млн км

Второй закон Кеплера . Радиус-вектор планеты за равные промежутки времени описывает равные площади.

Главное следствие второго закона Кеплера состоит в том, что во время движения планеты по орбите со временем меняется не только расстояние планеты до Солнца, но и ее линейная и угловая скорости.

Самую большую скорость планета имеет в перигелии, когда расстояние до Солнца наименьшее, а самую маленькую — в афелии, когда расстояние наибольшее.

Второй закон Кеплера фактически определяет известный физический закон сохранения энергии: сумма кинетической и потенциальной энергии в замкнутой системе является величиной постоянной. Кинетическая энергия определяется скоростью планеты, а потенциальная — расстоянием между планетой и Солнцем, поэтому при приближении к Солнцу скорость планеты возрастает (рис. 4.6).

Рис. 4.6. При приближении к Солнцу скорость планеты растет, а при удалении — уменьшается.

Если первый закон Кеплера проверить в условиях школы довольно трудно, ибо для этого нужно измерить расстояние от Земли до Солнца зимой и летом, то второй закон Кеплера может проверить любой ученик. Для этого надо убедиться, что скорость Земли в течение года меняется. Для проверки можно использовать обычный календарь и посчитать длительность полугодия от весеннего до осеннего равноденствия (21.03—23.09) и, наоборот, от 23.09 до 21.03. Если бы Земля вращалась вокруг Солнца с постоянной скоростью, то количество дней в этих полугодиях было бы одинаковым. Но согласно второму закону Кеплера, зимой скорость Земли больше, а летом — меньше, поэтому лето в Северном полушарии длится чуть больше, чем зима, а в Южном полушарии, наоборот, зима немного длиннее лета.

Максимальную скорость Земля имеет зимой -30,38 км/с.

Минимальную скорость Земля имеет летом – 29,36 км/с.

В июле Земля движется медленнее, поэтому продолжительность лета в Северном полушарии больше, чем в Южном. Этим объясняется, что среднегодовая температура Северного полушария Земли выше, чем Южного

Третий закон Кеплера. Квадраты сидерических периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.

где Т ₁ и Т ₂ — сидерический период обращения любых планет, и — большие полуоси орбит этих планет.

Если определить большую полуось орбиты какой-либо планеты или астероида, то, согласно третьему закону Кеплера, можно вычислить период обращения этого тела, не дожидаясь, пока оно сделает полный оборот вокруг Солнца. Например, в 1930 г. была открыта новая планета Солнечной системы — Плутон, которая имеет большую полуось орбиты 40 а. е., и сразу же был определен период обращения этой планеты вокруг Солнца — 248 лет. Правда, в 2006 г., согласно постановлению съезда Международного Астрономического Союза, Плутон перевели в статус планет-карликов, ибо его орбита пересекает орбиту Нептуна.

Рис. 4.7. Из наблюдений была определена большая полуось орбиты Плутона. Учитывая параметры орбиты Земли согласно 4.2, имеем Т ₂ = 248 л.

Третий закон Кеплера используется также и в космонавтике, если нужно определить период обращения вокруг Земли спутников или космических кораблей.

Закон всемирного тяготения

Великий английский физик и математик Исаак Ньютон доказал, что физической основой законов Кеплера является фундаментальный закон всемирного тяготения, который не только обусловливает движение планет в Солнечной системе, но и определяет взаимодействие звезд в Галактике. В 1687 г. Ньютон сформулировал этот закон так: любые два тела с массами Мum притягиваются с силой, величина которой прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними (рис. 4.8):

где G — гравитационная постоянная; R — расстояние между этими телами.

Рис. 4.8. Закон всемирного тяготения

Следует обратить внимание, что формула (4.3) справедлива только для двух материальных точек. Если тело имеет сферическую форму и плотность внутри распределена симметрично относительно центра, то массу такого тела можно считать материальной точкой, которая находится в центре сферы. Например, если космический корабль обращается вокруг Земли, то для определения силы, с которой корабль притягивается к Земле, принимают расстояние до центра Земли (рис. 4.9).

Рис. 4.9. Сила притяжения, действующая на космический корабль, зависит от расстояния R+H между кораблем и центром Земли

При помощи формулы (4.3) можно определить вес космонавтов на любой планете, если известен ее радиус R и масса М (рис. 4.10). Закон всемирного тяготения утверждает, что не только планета притягивается к Солнцу, но и Солнце притягивается с такой же силой к планете, поэтому движение двух тел в гравитационном поле происходит вокруг общего центра масс данной системы. То есть планета не падает на Солнце, потому что она движется с определенной скоростью по орбите, а Солнце не падает на планету под действием той же силы тяжести, ибо оно тоже обращается вокруг общего центра масс.

Вес космонавтов зависит от массы планеты и ее радиуса. На астероидах космонавты должны привязываться, чтобы не улететь в космическое пространство

В реальных условиях ни одна планета не движется по эллиптической орбите, ведь законы Кеплера справедливы только для двух тел, обращающихся вокруг общего центра масс. Известно, что в Солнечной системе обращаются вокруг Солнца большие планеты и множество малых тел, поэтому каждую планету притягивает не только Солнце — одновременно притягиваются между собой все эти тела. В результате такого взаимодействия разных по величине и направлению сил движение каждой планеты становится достаточно сложным. Такое движение называют возмущением. Орбита, по которой движется при возмущенном движении планета, не является эллипсом.

Благодаря исследованиям возмущения орбиты планеты Уран астрономы теоретически предсказали существование неизвестной планеты, которую в 1846 г. И. Галле обнаружил в рассчитанном месте. Планету назвали Нептуном.

Особенность закона всемирного тяготения заключается в том, что мы не знаем, каким образом передается на огромное расстояние притяжение между телами. Со времени открытия этого закона ученые придумали десятки гипотез о сути гравитационного взаимодействия, но наши знания сегодня ненамного больше, чем во времена Ньютона. Правда, физики открыли еще три удивительных взаимодействия между материальными телами, которые передаются на расстоянии: электромагнитное взаимодействие, сильное и слабое взаимодействие между элементарными частицами в атомном ядре. Среди этих видов взаимодействия гравитационные силы являются самыми слабыми. Например, по сравнению с электромагнитными силами гравитационное притяжение в 10 39 раз слабее, но только гравитация управляет движением планет, а также влияет на эволюцию Вселенной. Это можно объяснить тем, что электрические заряды имеют разный знак («+» и «-»), поэтому тела большой массы являются в основном нейтральными, и на большом расстоянии электромагнитное взаимодействие между ними довольно слабое.

Выводы

Все космические тела от планет до галактик движутся по закону всемирного тяготения, который был открыт Ньютоном. Законы Кеплера определяют форму орбиты, скорость движения планет Солнечной системы и их периоды обращения вокруг Солнца.

Астрономия. Базовый уровень. 11 класс: учебник / Б. А. Воронцов-Вельяминов, Е. К. Страут. – 5-е изд., пересмотр. – М.: Дрофа, 2018.

Астрономия. 11 класс. Методическое пособие к учебнику Б. А. Воронцова-Вельяминова, Е. К. Страута «Астрономия. Базовый уровень. 11 класс»/ М. А. Кунаш. — М.: Дрофа, 2018.

Н.Н. Гомулина. Открытая астрономия/ Под ред. В.Г. Сурдина. – Электронный образовательный ресурс. http://www.college.ru/astronomy/course/content/index.htm

В.Г. Сурдин. Астрономические задачи с решениями/ Издательство ЛКИ, 2017 г.

Вселенная в вопросах и ответах. Задачи и тесты по астрономии и космонавтике. В.Г. Сурдин. 2017

Сравнительные размеры крупнейших спутников Солнечной системы и планет Земной группы.

Срок, за который планеты совершают полный оборот вокруг Солнца, естественно различный. У Меркурия, самой ближней к звезде, он составляет 88 земных суток. Наша Земля проходит цикл за 365 дней и 6 часов. Самая крупная в Солнечной системе планета Юпитер завершает свой оборот за 11,9 земных лет. Ну а у Плутона, — наиболее удаленной от Солнца планеты оборот и вовсе составляет 247,7 года.

Следует также учесть, что все планеты в нашей Солнечной системе движутся, не вокруг светила, а вокруг так называемого центра масс. Каждая при этом, вращаясь вокруг своей оси, слегка раскачиваются (подобно юле). К тому же и сама ось может ненамного смещаться.

Похожие статьи

Понравилась запись? Расскажи о ней друзьям!

До Коперника

Траектория движения в пространстве

Представления о том, как расположены планеты на небосводе первым в своем трактате «Великое математическое построение по астрономии», высказал древнегреческий астроном Птолемей. Он первым предположил, что они совершают свои движения по кругу. Но Птолемей ошибочно считал, что все планеты, а также Луна и Солнце движутся вокруг Земли. До работы Коперника его трактат считался общепринятым как в арабском, так и западном мире.

Третий закон

Квадрат единого времени по орбитальной линии пропорционален кубическому параметру усреднённого расстояния от самой планеты до Солнца. Данная теория имеет ещё одно название, постулат часто именуют законом гармонии. В этом случае происходит сравнение орбитального отрезка времени с радиусом планетной орбиты. Таким образом, для каждой планеты соотношение квадратных показателей периодов движения и среднего расстояния, возведённого в куб, до светила аналогично.

Немецкий учёный Иоганн Кеплер был тем, кто открыл законы движения планет вокруг Солнца. Данные постулаты способствовали установлению формы орбитальных путей, позволяли рассчитать период обращения и скорость, а также наблюдать изменение показателей скорости на участках сближения и отдаления от Солнца. Учёный доказал, что Земля не является исключением и движется вокруг Солнца, соответствуя всем трём теориям, как и все остальные планеты в Солнечной системе.