Как нам улететь с Земли: краткое пособие для выезжающих за орбиту
Содержание
- 1 Как нам улететь с Земли: краткое пособие для выезжающих за орбиту
- 1.1 Как нам улететь с Земли: краткое пособие для выезжающих за орбиту
- 1.2 Что известно о космических скоростях простым людям
- 1.3 Вторая скорость для разных небесных тел
- 1.4 Третья космическая скорость
- 1.5 Что будет, если с Луны выстрелить в сторону Земли
- 1.6 Закон всемирного тяготения
- 1.7 Гравитация может также замедлить движение космического корабля
Как нам улететь с Земли: краткое пособие для выезжающих за орбиту
 Недавно на хабре появилась новость про планируемую постройку космического лифта. Для многих это показалось чем-то фантастическим и невероятным, вроде огромного кольца из Halo или сферы Дайсона. Но будущее ближе, чем кажется, лестница в небо вполне возможна, и может быть мы даже увидим ее на своем веку.
Недавно на хабре появилась новость про планируемую постройку космического лифта. Для многих это показалось чем-то фантастическим и невероятным, вроде огромного кольца из Halo или сферы Дайсона. Но будущее ближе, чем кажется, лестница в небо вполне возможна, и может быть мы даже увидим ее на своем веку.
Сейчас я постараюсь показать, почему мы не можем пойти и купить билет «Земля-Луна» по цене билета «Москва-Питер», как нам поможет лифт и за что он будет держаться, чтобы не рухнуть на землю.
С самого начала развития ракетостроения головной болью инженеров было топливо. Даже в самых современных ракетах топливо занимает где-то 98% массы корабля.
Если нам захочется передать космонавтам на МКС пакетик пряников массой в 1 килограмм, то на это потребуется, грубо говоря, 100 килограмм ракетного топлива. Ракета-носитель одноразовая, и на Землю вернется только в виде обгоревших обломков. Дорогие получаются прянички. Масса корабля ограничена, а значит и полезный груз на один запуск строго лимитирован. И каждый запуск требует расходов.
А если мы хотим полететь куда-то дальше околоземной орбиты?
Инженеры со всего мира сели и стали думать: каким должен быть космический корабль, чтобы увезти на нем больше, и долететь на нем дальше?
Куда долетит ракета?
Пока инженеры думали, их дети нашли где-то селитру и картон и начали мастерить игрушечные ракеты. Такие ракеты не долетали до крыш высотных домов, но дети радовались. Потом самому смышленому пришла мысль: «а давайте натолкаем в ракету больше селитры, и она полетит выше».
Но выше ракета не полетела, так как стала слишком тяжелой. Она даже не смогла подняться в воздух. После некоторого количества экспериментов дети нашли оптимальный объем селитры, при котором ракета летит выше всего. Если добавить больше топлива, масса ракеты тянет ее вниз. Если меньше — топливо заканчивается раньше.
Инженеры тоже быстро сообразили, что если мы хотим залить больше топлива, значит и сила тяги должна быть больше. Вариантов увеличить дальность полета немного:
- увеличить КПД двигателя, чтобы потери топлива были минимальными (сопло Лаваля)
- увеличить удельный импульс топлива, чтобы при равной массе топлива сила тяги была больше
Хотя инженеры постоянно продвигаются вперед, практически всю массу корабля занимает топливо. Так как кроме топлива хочется отправить в космос что-нибудь полезное, весь путь ракеты тщательно просчитывается, и топлива в ракету закладывают самый минимум. При этом активно пользуются гравитационной помощью небесных тел и центробежными силами. Космонавты после завершения миссии не говорят: «ребята, в баке еще осталось немного топлива, давайте слетаем на Венеру».
Но как определить, сколько топлива нужно, чтобы ракета не упала в океан с пустым баком, а долетела до Марса?
Вторая космическая скорость
Дети тоже пытались заставить ракету лететь выше. Даже раздобыли учебник по аэродинамике, прочитали про уравнения Навье-Стокса, но ничего не поняли и просто приделали ракете острый нос.
Мимо проходил их знакомый старик Хоттабыч и поинтересовался, о чем грустят ребята.
— Эх, дедушка, если бы у нас была ракета с бесконечным топливом и малой массой, она бы наверное долетела до небоскреба, или даже до самой вершины горы.
— Не беда, Костя-ибн-Эдуард, — ответил Хоттабыч, выдергивая последний волосок, — пусть у этой ракеты топливо никогда не заканчивается.
Радостные дети запустили ракету и стали ждать, когда она вернется на землю. Ракета долетела и до небоскреба, и до вершины горы, но не остановилась и полетела дальше, пока не пропала из вида. Если заглянуть в будущее, то эта ракета покинула землю, вылетела из солнечной системы, нашей галактики и полетела на субсветовой скорости покорять просторы вселенной.
Дети удивились, как это их маленькая ракета смогла так далеко улететь. Ведь в школе говорили, что для того чтобы не упасть обратно на Землю, скорость должна быть не меньше второй космической (11,2 км/с). Разве их маленькая ракета могла развить такую скорость?
Но их родители-инженеры объяснили, что если у ракеты бесконечный запас топлива, то она сможет улететь куда угодно, если сила тяги больше гравитационных сил и сил трения. Так как ракета способна взлететь, силы тяги хватает, а в открытом космосе еще легче.
Вторая космическая скорость — это не скорость, которая должна быть у ракеты. Это скорость, с которой нужно бросить мяч с поверхности земли, чтобы он на нее не вернулся. У ракеты, в отличие от мяча, есть двигатели. Для нее важна не скорость, а суммарный импульс.
Самое сложное для ракеты — преодолеть начальный участок пути. Во-первых, гравитация у поверхности сильнее. Во-вторых, у Земли плотная атмосфера, в которой очень жарко летать на таких скоростях. Да и реактивные ракетные двигатели работают в ней хуже, чем в вакууме. Поэтому летают сейчас на многоступенчатых ракетах: первая ступень быстро расходует свое топливо и отделяется, а облегченный корабль летит на других двигателях.
Константин Циолковский долго думал над этой проблемой, и придумал космический лифт (еще в 1895 году). Над ним тогда, конечно, посмеялись. Впрочем, посмеялись над ним и из-за ракеты, и спутника, и орбитальных станций, и вообще посчитали его не от мира сего: «у нас тут еще автомобили не до конца изобретены, а он в космос собрался».
Потом ученые задумались и прониклись, полетела ракета, запустили спутник, понастроили орбитальных станций, в которые заселили людей. Над Циолковским уже никто не смеется, наоборот, его очень уважают. А когда открыли сверхпрочные графеновые нанотрубки, всерьез задумались и о «лестнице в небо».
Почему спутники не падают вниз?
Все знают про центробежную силу. Если быстро крутить мячик на веревочке, он не падает на землю. Попробуем быстро раскрутить мяч, а затем постепенно замедлим скорость вращения. В какой-то момент он перестанет крутиться и упадет. Это будет минимальная скорость, при которой центробежная сила будет уравновешивать силу притяжения земли. Если крутить мяч быстрее, веревка сильнее натянется (а в какой-то момент лопнет).
Между Землей и спутниками тоже есть «веревка» — гравитация. Но в отличие от обычной веревки она не может натягиваться. Если «крутить» спутник быстрее чем нужно, он «оторвется» (и перейдет на эллиптическую орбиту, или вообще улетит). Чем ближе спутник к поверхности земли, тем быстрее его нужно «крутить». Мяч на короткой веревке тоже крутится быстрее, чем на длинной.
Важно помнить, что орбитальная (линейная) скорость спутника — это не скорость относительно поверхности земли. Если написано, что орбитальная скорость спутника 3.07 км/с, это не значит, что он носится над поверхностью как бешеный. Орбитальная скорость точек на экваторе земли, между прочим, 465 м/с (Земля вертится, как утверждал упрямый Галилей).
На самом деле для мяча на веревочке и для спутника рассчитываются не линейные скорости, а угловые (сколько оборотов в секунду совершает тело).  Получается, если найти такую орбиту, что угловые скорости спутника и поверхности земли будут совпадать, то спутник будет висеть над одной точкой на поверхности. Такую орбиту нашли, и она называется геостационарная орбита (ГСО). Спутники висят над экватором неподвижно, и людям не приходится поворачивать тарелки и «ловить сигнал».
Получается, если найти такую орбиту, что угловые скорости спутника и поверхности земли будут совпадать, то спутник будет висеть над одной точкой на поверхности. Такую орбиту нашли, и она называется геостационарная орбита (ГСО). Спутники висят над экватором неподвижно, и людям не приходится поворачивать тарелки и «ловить сигнал».
Бобовый стебель
А что, если спустить с такого спутника веревочку до самой земли, ведь он висит над одной точкой? К другому концу спутника привязать груз, центробежная сила увеличится и будет держать и спутник, и веревочку. Ведь не падает мяч, если его хорошо раскрутить. Тогда можно будет поднимать по этой веревочке грузы прямо на орбиту, и забыть как страшный сон многоступенчатые ракеты, жрущие топливо килотоннами при небольшой грузоподъемности.
Скорость движения в атмосфере у груза будет небольшая, значит нагреваться он не будет, в отличие от ракеты. И энергии на подъем потребуется меньше, так как есть точка опоры.
Главная проблема — масса веревочки. До геостационарной орбиты Земли 35 тысяч километров. Если дотянуть до геостационарной орбиты стальную леску диаметром 1 мм, ее масса будет 212 тонн (а ее нужно тянуть гораздо дальше, чтобы уравновесить лифт центробежной силой). При этом она должна выдерживать свой вес, и вес груза.
К счастью, в этом случае немного помогает то, за что учителя по физике часто ругают учеников: вес и масса — разные вещи. Чем дальше тянется трос от поверхности земли, тем больше он теряет в весе. Хотя удельная прочность троса всё еще должна быть огромной.
С углеродными нанотрубками у инженеров появилась надежда. Сейчас это новая технология, и мы пока не можем свить эти трубочки в длинный трос. И не получается добиться их максимальной расчетной прочности. Но кто знает, что будет дальше?
Что известно о космических скоростях простым людям
На телевидении есть передача, в которой весёлый молодой человек бегает по улицам и задаёт прохожим разные вопросы. За правильный ответ он вручает 1000 рублей. Однажды он задал такой вопрос: «Какую скорость надо развить, чтобы оторваться от Земли?» Первый встречный ответить не смог, и ведущий буквально клещами вытащил из второго ответ, который был признан правильным: «Вторую космическую».
Увы, молодой человек ошибся. Вернее, ошибся не он, а редакторы, придумывающие вопросы и ответы к ним. Точно так, как и редакторы, считают почти все, кто хоть отдалённо слышал про существование первой и второй космических скоростей.
На самом деле, чтобы оторваться от Земли, подходит любая скорость. Уже когда ребёнок подпрыгивает, он отрывается от Земли. Пусть ненадолго, но отрывается. И вообще, до Луны или до другого космического объекта можно добраться с любой скоростью. Для этого надо немного разогнаться, а потом поддерживать силу тяги двигателя, равную силе земного притяжения, и вы будете «бороздить просторы Вселенной» с постоянной скоростью. Более того, если представить, что какой-то чудак сумел построить лестницу до Луны, то вы сможете подняться туда просто пешком. Примерно так, как вы поднимаетесь к себе домой на третий этаж, только гораздо дольше.
А как же космические скорости? Космические скорости подразумевают, что ракета, достигнув их, дальше летит к намеченной цели по инерции, с неработающим двигателем. Это только в мультфильмах про космические путешествия показывают летящие ракеты с работающим двигателем. Но это исключительно для создания иллюзии движения.
Если же в реальных условиях двигатель у ракеты будет работать постоянно, то даже для полёта на Луну потребуется такое количество топлива, что его ни одна ракета не осилит.
Вторая скорость для разных небесных тел
Итак, попробуем на основании выведенной формулы рассчитать вторую космическую скорость для разных небесных тел Солнечной Системы, учитывая что их радиус и массу мы знаем.
Начнем с самого простого – Земли. Радиус нашей планеты равен 6,37 тысяч километров, а масса – 5,97 х 10²³ кг. Подставляем в нашу формулу и получаем – вторая космическая скорость Земли равна 11,2 километра в секунду. Именно до таких цифр нужно разогнать гипотетический объект, чтобы он покинул зону гравитационного притяжения нашей планеты.
Теперь можно перейти к нашей звезде и посчитать вторую космическую скорость для Солнца. Радиус его равен 696 тысяч километров, а масса 1,989 х 10³⁰ кг. Расчеты по формуле дают результат в 617,7 километров в секунду! До такой скорости нужно разогнать предмет, чтобы он смог покинуть нашу Солнечную Систему и попасть в межзвездное пространство.
Теперь попробуем вычислить показатель для остальных планет системы. Итак, радиус и масса Меркурия составляют соответственно 2,438 тысяч километров и 330 х 10²¹ кг. Подставив в формулу цифры, получаем вторую космическую скорость Меркурия 4,3 км/с.
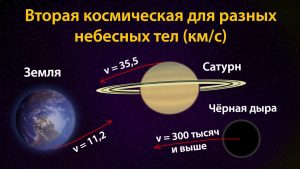
Идем далее и получаем такие цифры – вторая космическая скорость Венеры – 11,2 километров в секунду, Марса – 5,0 км/с, Юпитера – 61 км/с, Сатурна – 36 км/с, Нептуна – 24 км/с, Урана – 22 км/с, Луна – 2,4 км/с.
Таким образом, мы видим, что преимущественно чем массивнее планета (а вернее, чем плотнее, потому что радиус тоже важен) – тем больше нужна скорость, чтобы объект мог вырваться за пределы гравитационного влияния.
Показательными и интересными также являются примеры третей и четвертой космических скоростей. Что это за параметры? Если говорить грубо – то третья космическая скорость, это вторая космическая для Солнца, но высчитываемая вблизи Земли. Простыми словами – какую скорость нужно развить с Земли, чтобы покинуть Солнечную Систему? Посчитав по формуле, получим 16,65 километров в секунду.
 Четвертая космическая скорость показывает, до какой цифры нужно разогнаться чтобы покинуть галактику из заданной точки. Для Млечного пути этот показатель будет разным в зависимости от выбранной координаты. Ближе к центральной сверхмассивной черной дыре он будет гигантским, ближе к периферии галактики – меньше. Примерно в области нашей Солнечной Системы четвертая космическая скорость равна 550 километрам в секунду!
Четвертая космическая скорость показывает, до какой цифры нужно разогнаться чтобы покинуть галактику из заданной точки. Для Млечного пути этот показатель будет разным в зависимости от выбранной координаты. Ближе к центральной сверхмассивной черной дыре он будет гигантским, ближе к периферии галактики – меньше. Примерно в области нашей Солнечной Системы четвертая космическая скорость равна 550 километрам в секунду!
Похожие статьи
Понравилась запись? Расскажи о ней друзьям!
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.

Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Что будет, если с Луны выстрелить в сторону Земли
Вопрос довольно необычный, ведь вряд ли кому-то в голову придет совершить подобное. Однако в данном случае ответ интересен с точки зрения физических законов.
Что если астронавт, находясь на Луне, выстрелит в сторону Земли? Долетит ли пуля до поверхности планеты?
Пуля и вторая космическая скорость
Казалось бы, скорость пули довольно высока, а гравитация Луны невелика – в шесть раз меньше земной. В связи с чем, она не способна даже удерживать выделяемые из под ее поверхности газы и потому практически не имеет своей атмосферы. Исходя из вышесказанного, можно прийти к выводу, что выстрел, произведенный с поверхности спутника, может иметь последствия на поверхности Земли.
Однако все не так просто. Чтобы какой-либо объект мог оторваться от поверхности небесного тела и выйти в открытый космос, преодолев его гравитацию, ему необходимо набрать определенную скорость. Она рассчитывается по специальной формуле, и для каждой планеты или спутника она разная.
В физике это понятие носит название второй космической скорости. Так, чтобы взлететь с Луны, объект должен разогнаться до 2,38 км/с. Однако скорость обычной пули не может превышать и 1000 м/с.
Связано это с тем, что в случае более высокой скорости целостность выстрелившего оружия будет нарушена. Потому что такой прочности достичь крайне сложно. К тому же, чем выше скорость пули, тем сильнее сопротивление воздуха.
В связи с этим, свинец, из которого состоит снаряд, нагреется до температуры плавления и, в конечном счете, потеряет форму. При этом, более термостойкие металлы не используются в производстве пуль из соображений экономии и снижения себестоимости. И даже сверхскоростные патроны, такие как .220 Winchester Swift вылетают из оружейного ствола со скоростью, не превышающей 1,2 км/с.
Этого недостаточно для того, чтобы пуля преодолела гравитацию Луны и вышла в космос. Также начальная скорость современных артиллерийских снарядов чуть больше 1000 м/с. Поэтому обычное оружие на Луне для Земли совершенно безвредно.
Однако благодаря новейшим технологиям, люди смогли создать оружие, для которого скорость не является существенной проблемой. Так как принцип его механизма обусловлен работой электромагнитных сил. Их создают с помощью короткого замыкания двух параллельных рельсов, несущих ток.
Данное оружие способно выпустить снаряд со скоростью более 6 км/с. Этого вполне достаточно, чтобы покинуть пределы Луны. Но, чтобы попасть точно в Землю, необходимо постараться. Ведь в пределах космоса Земля довольно мала.
Если промахнуться, снаряд станет спутником планеты. Однако даже в случае успеха, он столкнется с плотной атмосферой Земли и расплавится, так и не достигнув поверхности.
Закон всемирного тяготения
Законы Кеплера — это результаты наблюдений и обобщений. Теоретически их обосновал Исаак Ньютон в законе всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон всемирного тяготения
F — сила тяготения [Н]
M — масса первого тела (часто планеты) [кг]
m — масса второго тела [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
G = 6,67 × 10 -11 м 3 ·кг -1 ·с -2
Ньютон был первым исследователем, который пришел к выводу, что между любыми телами в космосе действуют гравитационные силы, и именно они определяют характер движения этих тел.
Гравитация может также замедлить движение космического корабля
Кроме того, гравитационные силы могут использоваться для замедления движения космического корабля вместо ускорения его. В примере выше рассмотрим, что космический корабль приближается к планете в направлении, противоположном её движению по орбите вокруг Солнца. Таким образом, математика будет работать так, что скорость космического корабля уменьшается после сближения с планетой. Космический аппарат NASA Messenger использовал гравитацию Земли и Венеры, чтобы замедлить свое движение таким образом, что он мог быть захвачен Меркурием и остался на его орбите.
В научно-фантастическом романе «Свидание с Рамой» Артур Кларк описывает инопланетную цивилизацию, чей межзвездный космический корабль использует гравитацию нашего Солнца для выполнения своего межзвездного маневра, заставляя людей волноваться и думать об этом процессе.